
study guide and intervention trigonometry 8 4
Trigonometry studies relationships between angles and sides of triangles, essential for various fields like engineering, physics, and astronomy, providing foundational concepts for problem-solving.
Definition of Trigonometric Ratios

Trigonometric ratios relate the angles of a right triangle to the lengths of its sides. The three primary ratios are sine (sin), cosine (cos), and tangent (tan). Sine is the ratio of the length of the opposite side to the hypotenuse, while cosine is the adjacent side to the hypotenuse. Tangent is the opposite side to the adjacent side. These ratios are fundamental for solving problems involving right triangles and are often remembered using the mnemonic SOHCAHTOA (Sine = Opposite/Hypotenuse, Cosine = Adjacent/Hypotenuse, Tangent = Opposite/Adjacent). Understanding these ratios is crucial for applying trigonometry in real-world scenarios and advanced mathematical studies.
Importance of Trigonometry in Real-World Applications
Trigonometry plays a vital role in various real-world applications, making it an essential tool in multiple fields. In engineering, it is used to calculate distances, heights, and angles, aiding in the design of structures and machines. Physics relies on trigonometric ratios to analyze wave patterns and forces. Navigation systems, such as GPS, use trigonometry to determine precise locations and paths. Additionally, astronomy uses trigonometric functions to study the positions and movements of celestial bodies. Even in medicine, trigonometry is applied in imaging technologies like MRI and CAT scans. Understanding trigonometry is not only crucial for academic success but also for solving practical problems in diverse industries, demonstrating its wide-ranging importance.
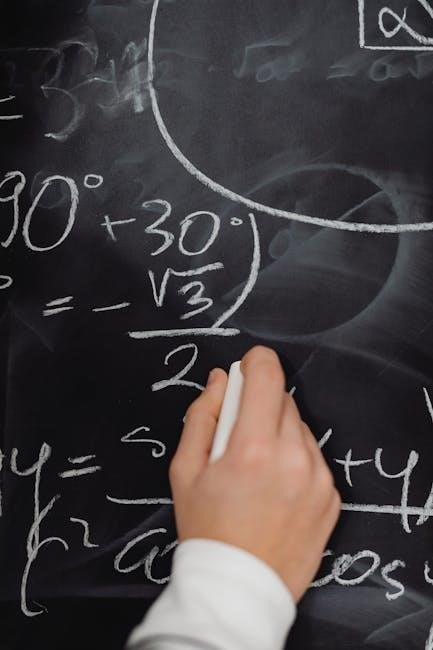
Trigonometric Ratios
Trigonometric ratios relate angles to side lengths in right triangles. Sine (sin), cosine (cos), and tangent (tan) are defined as opposite/hypotenuse, adjacent/hypotenuse, and opposite/adjacent, respectively.

Sine, Cosine, and Tangent Explained
In trigonometry, sine, cosine, and tangent are fundamental ratios used to describe the relationships between angles and side lengths in right triangles. Sine (sin) of an angle is the ratio of the length of the opposite side to the hypotenuse. Cosine (cos) is the ratio of the adjacent side to the hypotenuse. Tangent (tan) is the ratio of the opposite side to the adjacent side. These ratios are essential for solving problems involving angles and triangles. For example, if a triangle has an angle θ, sin θ = opposite/hypotenuse, cos θ = adjacent/hypotenuse, and tan θ = opposite/adjacent. These definitions form the basis for solving various trigonometric problems.
Using SOHCAHTOA for Remembering Ratios
SOHCAHTOA is a popular mnemonic device used to remember the trigonometric ratios of sine, cosine, and tangent. Each letter in the word represents the first letter of a word that corresponds to the ratios: Sine = Opposite over Hypotenuse, Cosine = Adjacent over Hypotenuse, and Tangent = Opposite over Adjacent. This tool helps students associate the ratios with their respective sides in a right triangle. By creating a memorable sentence like “Sally’s Cats Always Hunt Those Angry Dogs,” learners can easily recall the ratios. This method simplifies the process of identifying and applying the correct ratio when solving trigonometric problems, making it a valuable study aid for mastering trigonometry.
Right Triangle Relationships
In a right triangle, the relationships between the sides and angles are fundamental to trigonometry. The Pythagorean theorem, (a^2 + b^2 = c^2), relates the lengths of the legs (a and b) to the hypotenuse (c). The trigonometric ratios—sine, cosine, and tangent—are defined based on these side lengths. For any acute angle, sine is the ratio of the opposite side to the hypotenuse, cosine is the adjacent side to the hypotenuse, and tangent is the opposite side to the adjacent side. These relationships allow for the calculation of unknown sides and angles in right triangles, making them essential tools in various applications such as engineering and physics. Understanding these connections is crucial for solving problems involving right triangles.

Angles of Elevation and Depression
Angles of elevation and depression involve measuring vertical angles from the horizontal, crucial for determining heights and distances in various real-world trigonometric applications and problem-solving scenarios.
Understanding Angles of Elevation
An angle of elevation is the angle formed by a horizontal line and a line of sight raised to an object above. It is measured from the horizontal to the line of sight. This concept is essential in trigonometry for determining heights and distances in real-world scenarios, such as construction or physics. For example, if Sarah sights the top of a cliff at a 60° angle of elevation, trigonometric ratios can be used to calculate the cliff’s height or distance. Understanding angles of elevation involves visualizing the triangle formed and applying sine, cosine, or tangent to find unknown sides. This skill is critical for solving practical problems involving heights and slopes.

Understanding Angles of Depression
An angle of depression is the angle formed by a horizontal line and a line of sight directed downward to an object below. It is measured from the horizontal to the line of sight. This concept is crucial in trigonometry for determining depths and distances in real-world scenarios, such as engineering or physics. For instance, if a pilot measures the angle of depression to a runway, trigonometric ratios can calculate the plane’s altitude or distance. Understanding angles of depression involves visualizing the triangle formed and applying sine, cosine, or tangent to find unknown sides. This skill is vital for solving practical problems involving depths and downward slopes, mirroring the application of angles of elevation but in the opposite direction.
Real-World Problems Involving Elevation and Depression
Angles of elevation and depression are essential in solving practical problems across various fields. For instance, surveyors use these angles to measure heights and distances between landmarks. Pilots rely on angles of depression to determine their altitude above the ground and distances to runways. In construction, workers use these concepts to ensure structures are level or to calculate slopes. Trigonometric ratios like sine, cosine, and tangent are applied to find unknown sides or angles in these scenarios. These problems highlight the importance of trigonometry in real-world applications, making it a foundational skill for careers in engineering, physics, and more. Mastering these concepts enables accurate calculations for real-life challenges, showcasing trigonometry’s practical relevance.

Inverse Trigonometric Ratios
Inverse trigonometric ratios allow finding angles when given the ratios of sides in a right triangle, using functions like arcsin, arccos, and arctan to solve for unknown angles.
Using Inverse Sine, Cosine, and Tangent
Inverse trigonometric functions—arcsin, arccos, and arctan—allow users to find angles when side ratios are known. For example, if the opposite side is 3 and the hypotenuse is 5, arcsin(3/5) calculates the angle. These functions are essential for solving real-world problems, such as determining heights or distances in various fields. The ranges of inverse functions are specific: arcsin and arctan range from -90° to 90°, while arccos ranges from 0° to 180°, ensuring one-to-one outputs. When using calculators, input the ratio, select the appropriate inverse function, and interpret the result within the correct range. This process aids in accurately finding missing angles in right triangles, avoiding common errors like invalid input ranges. These tools are invaluable in trigonometry, offering practical applications across multiple disciplines.
Solving Problems with Inverse Ratios
Inverse trigonometric ratios are used to find missing angles in right triangles when side lengths are known. For example, if the opposite side is 5 and the adjacent side is 12, arctan(5/12) calculates the angle. To solve problems, set up the ratio, apply the appropriate inverse function, and calculate the angle. Ensure the calculator is in the correct mode (degrees or radians). When interpreting results, consider the context of the problem to ensure the angle is reasonable. Common errors include invalid input ranges or mismatched modes. Always verify the solution by plugging the angle back into the original ratio. This method is essential for real-world applications, such as determining heights or distances, and builds a strong foundation for more complex trigonometric problem-solving.

Special Products
Special products involve squaring sums or differences, useful in trigonometry to simplify expressions. These formulas expand binomials, aiding in problem-solving and equation simplification effectively.
Squares of Sums and Differences
The squares of sums and differences are algebraic identities used to expand expressions. The square of a sum, (a + b)², equals a² + 2ab + b², while the square of a difference, (a ⸺ b)², equals a² ⸺ 2ab + b². These formulas are essential for simplifying expressions in trigonometry, particularly when dealing with angle addition or subtraction problems. For example, in trigonometric identities, squaring sums or differences helps break down complex expressions into manageable parts. By mastering these special products, students can solve equations more efficiently and understand how angles and sides relate in various trigonometric scenarios.

Applications of Special Products in Trigonometry
Special products, like squares of sums and differences, are vital in trigonometry for simplifying expressions and solving equations. These identities help in expanding and factoring terms, which is crucial for proving trigonometric identities and solving complex problems. For instance, they are used in deriving formulas for sin(A ± B) and cos(A ± B), which are fundamental in wave phenomena and vector addition. Additionally, these products aid in solving real-world problems, such as calculating distances in navigation or analyzing periodic functions in physics. Mastery of these concepts enhances problem-solving skills and deepens understanding of trigonometric relationships.

Study Guide and Intervention Strategies
This guide offers structured approaches to mastering trigonometry, including practice exercises, mnemonic devices, and targeted interventions to address common challenges and reinforce key concepts effectively.
Effective Study Techniques for Trigonometry
- Engage in active learning by drawing and measuring right triangles to visualize trigonometric ratios.
- Use mnemonic devices like SOHCAHTOA to remember sine, cosine, and tangent definitions.
- Practice regularly with exercises from the study guide, focusing on inverse ratios and special products.
- Break down complex problems into smaller, manageable steps for better understanding.
- Apply trigonometric concepts to real-world scenarios to enhance problem-solving skills.
- Join study groups to collaborate and discuss challenging topics.
- Seek immediate help when struggling with a concept to avoid gaps in knowledge.
- Review notes and textbook chapters consistently to reinforce learning.
Intervention Techniques for Common Challenges
To address difficulties in trigonometry, consider the following strategies:
- Use visual aids like graphs and diagrams to simplify complex concepts.
- Break problems into smaller, step-by-step tasks to reduce overwhelm.
- Apply real-world examples to make abstract ideas more relatable.
- Incorporate technology, such as calculators and educational software, for interactive learning.
- Encourage peer tutoring and group work to foster collaborative problem-solving.
- Provide one-on-one support for students struggling with specific topics.
- Offer extra practice exercises and review sessions to reinforce understanding.
- Use positive reinforcement to build confidence and motivation.